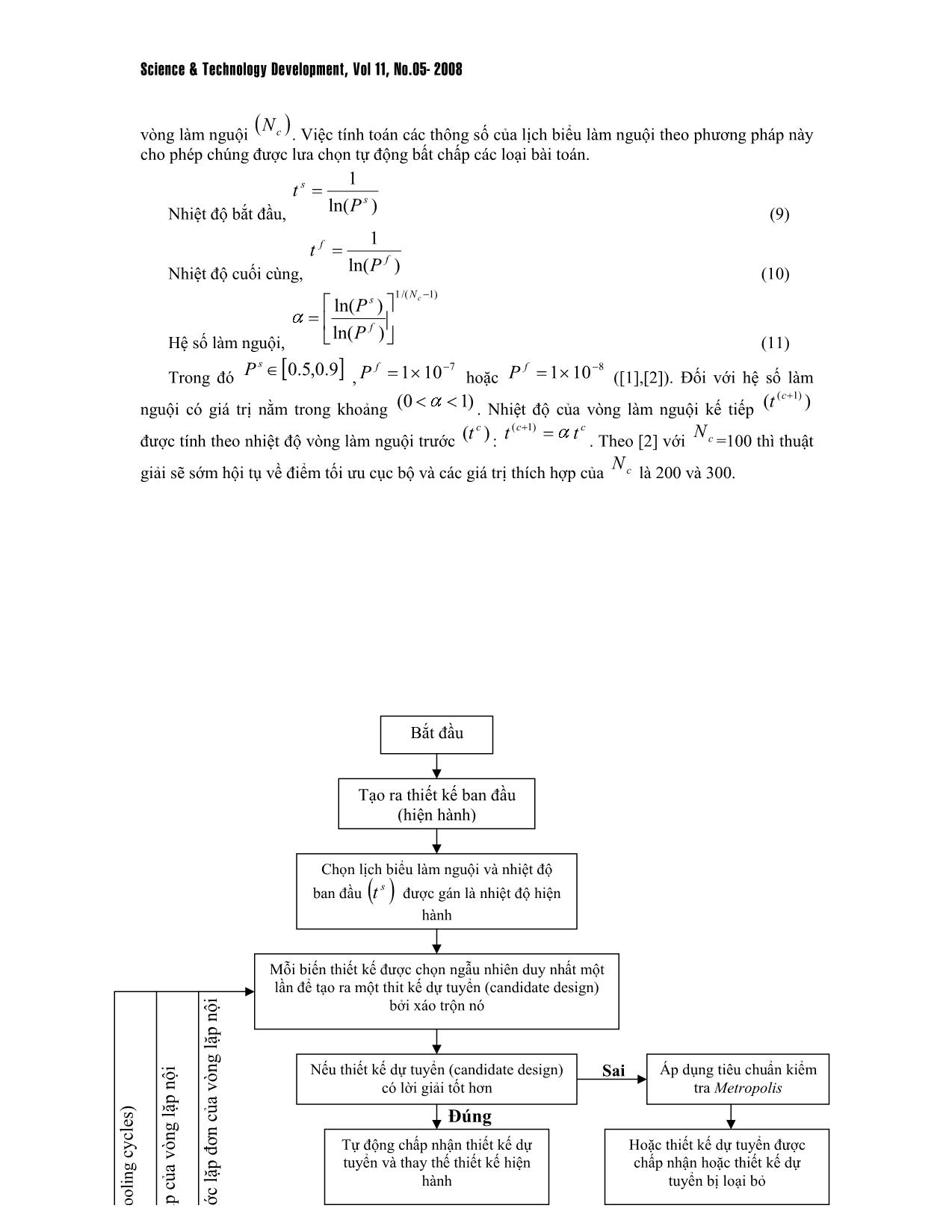
Tối ưu vị tướng của kết cấu dàn phẳng sử dụng thuật giải mô phỏng luyện kim

Bài toán tối ưu vị tướng (Topology optimization) kết cấu dàn chủ yếu được phát biểu trong

giới hạn của phương pháp kết cấu nền (ground structure approach) được đề nghị đầu tiên bởi

Dorn [8].Trong phương pháp này, quá trình tìm kiếm bắt đầu từ một kết cấu nền ban đầu được tạo

ra bởi một tập hợp n các điểm nút cho trước và n(n -1) / 2 liên kết thanh có thể giữa các nút

(Hình.1). Các phương pháp số được sử dụng để loại bỏ các thanh không cần thiết trong kết cấu

nền ban đầu này để tìm ra một kết cấu dàn tối ưu. Các phương pháp qui hoạch phi tuyến

(nonlinear programming) truyền thống chỉ ứng dụng thành công trong các bài toán nhỏ và rất khó

khăn để tìm ra lời giải tối ưu toàn cục. Gần đây, một số lượng các phương pháp tối ưu toàn cục

nổi lên như là những thuật toán triển vọng để giải quyết các bài toán tối ưu phức tạp. Các phương

pháp phổ biến nhất bao gồm: Thuật giải di truyền, mô phỏng luyện kim (SA), tabu search