Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 5: Tối ưu hàm nhiều biến số với ràng buộc bất đẳng thức. Phương pháp cổ điển
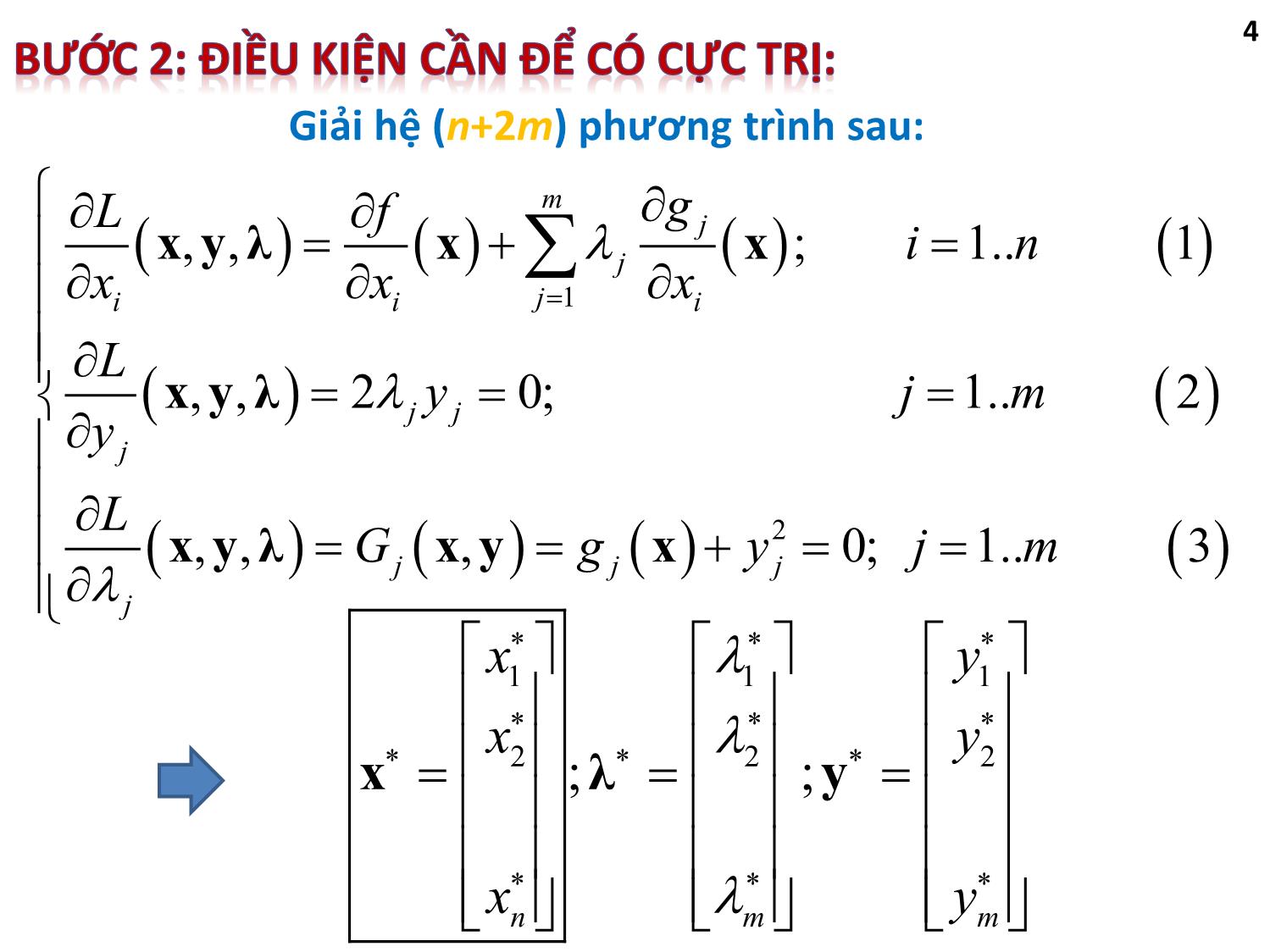
- Phương trình (3) để đảm bảo các điều kiện gj(x) ≤ 0
được thỏa mãn
- Phương trình (2) cho ra kết quả hoặc là λj = 0, hoặc là
yj = 0
- Nếu λ
j = 0 thì có nghĩa là ràng buộc thứ j không cần dùng tới và nó có thể được bỏ qua
- Nếu yj = 0 thì có nghĩa là ràng buộc gj(x)=0 hoạt động tại ngay điểm cực trị
Ta có thể chia các ràng buộc ra 2 tập hợp con:
Tập hợp j ϵ J1 khi yj = 0 (ràng buộc hoạt động ngay điểm cực trị, λj ≠ 0 )
Tập hợp j ϵ J2 khi λj = 0 (ràng buộc được bỏ qua)
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 5: Tối ưu hàm nhiều biến số với ràng buộc bất đẳng thức. Phương pháp cổ điển trang 1
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 5: Tối ưu hàm nhiều biến số với ràng buộc bất đẳng thức. Phương pháp cổ điển trang 2
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 5: Tối ưu hàm nhiều biến số với ràng buộc bất đẳng thức. Phương pháp cổ điển trang 3
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 5: Tối ưu hàm nhiều biến số với ràng buộc bất đẳng thức. Phương pháp cổ điển trang 4
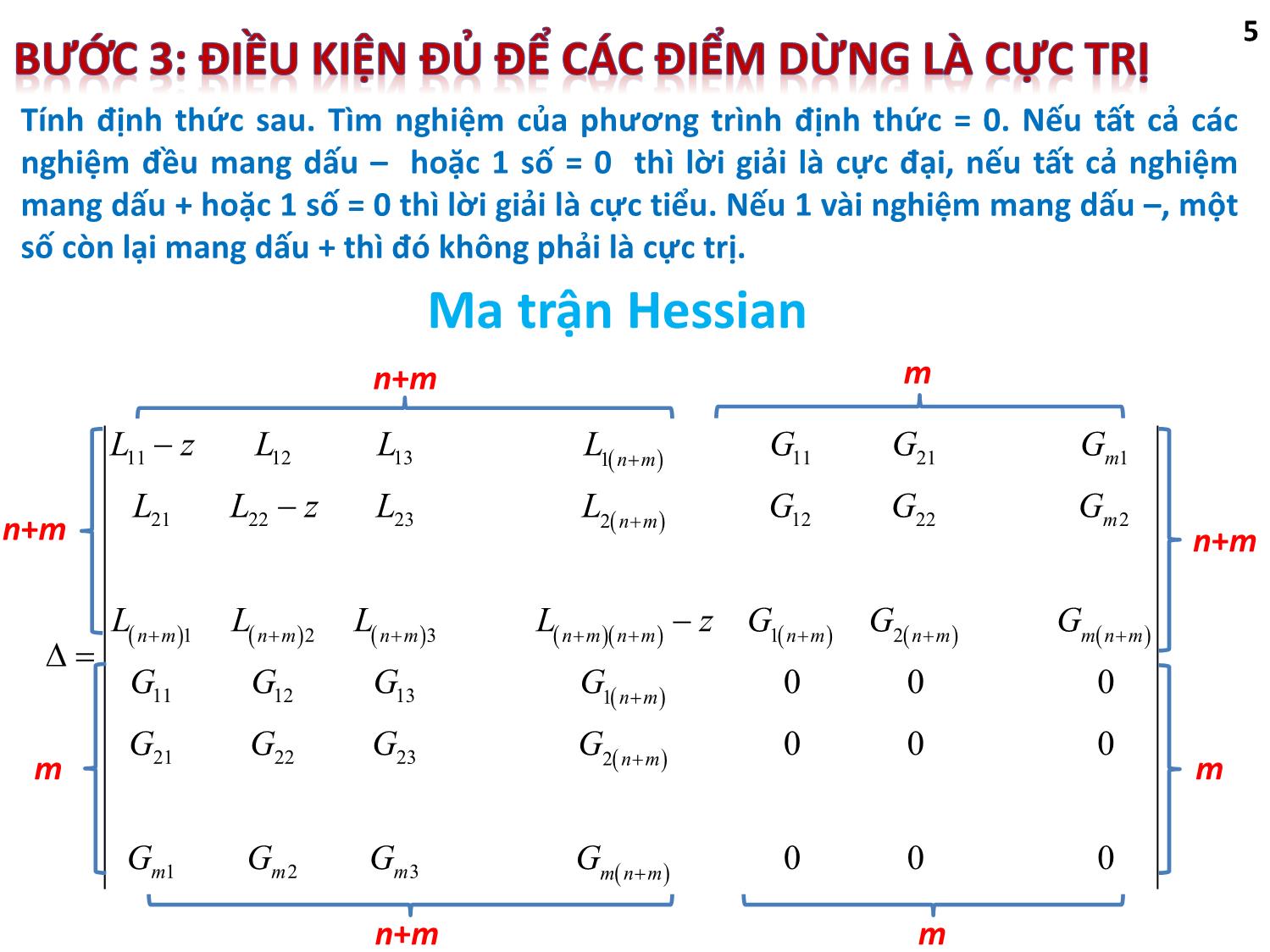
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 5: Tối ưu hàm nhiều biến số với ràng buộc bất đẳng thức. Phương pháp cổ điển trang 5
Tải về để xem đầy đủ hơn
File đính kèm:
bai_giang_toi_uu_hoa_trong_thiet_ke_co_khi_chuong_5_toi_uu_h.pdf
