Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 3: Tối ưu hàm nhiều biến số không có ràng buộc
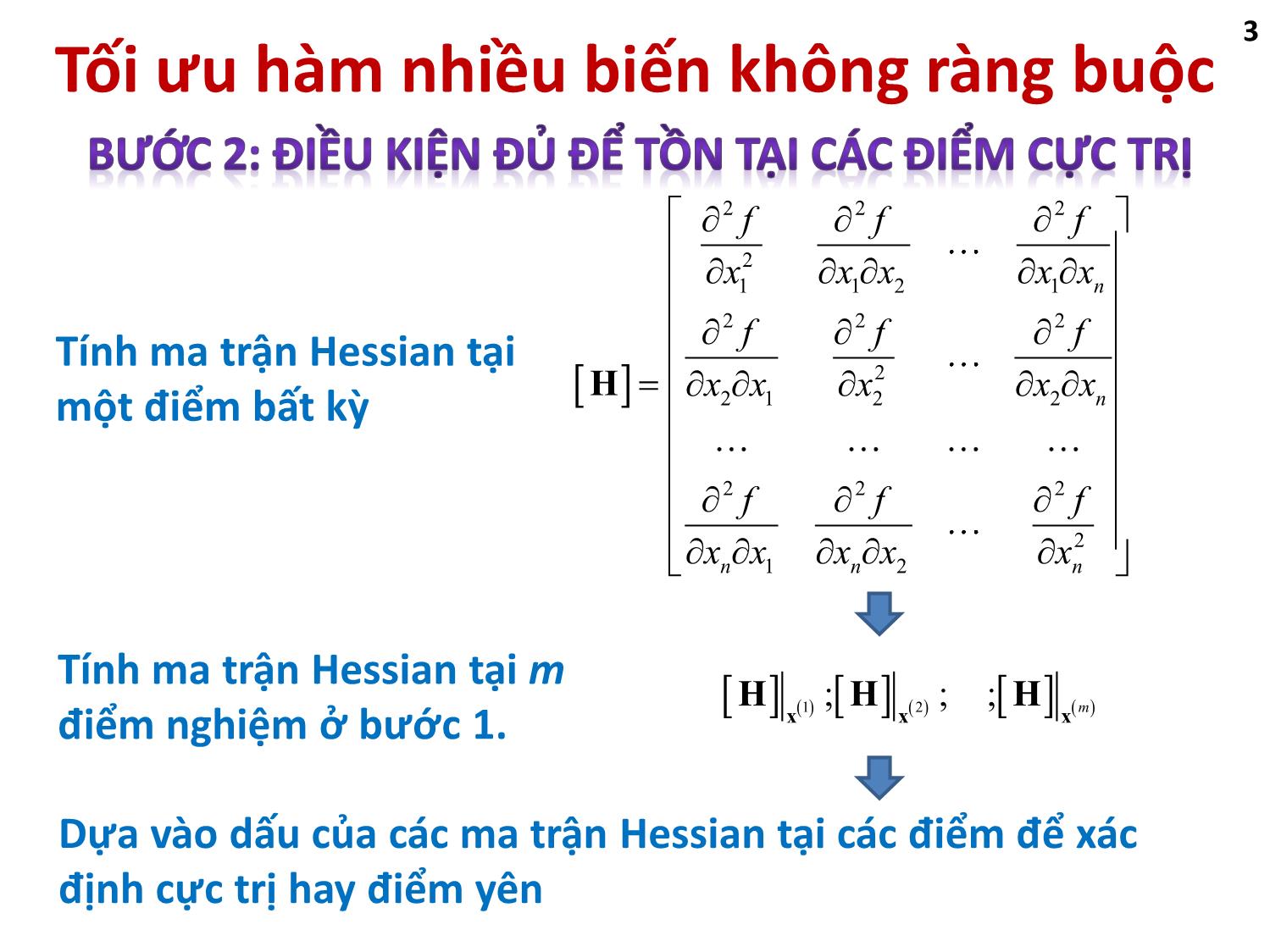
Giả sử ma trận Hessian tại điểm nghiệm i có dạng
Tính định thức của n ma trận thành phần:
1. Nếu tất cả A
1, A2, , An > 0 thì ma trận [H] > 0 x(i) – cực tiểu
2. Nếu dấu của A
j là (–1)j (j=1.n) thì [H] < 0 x(i) – cực đại
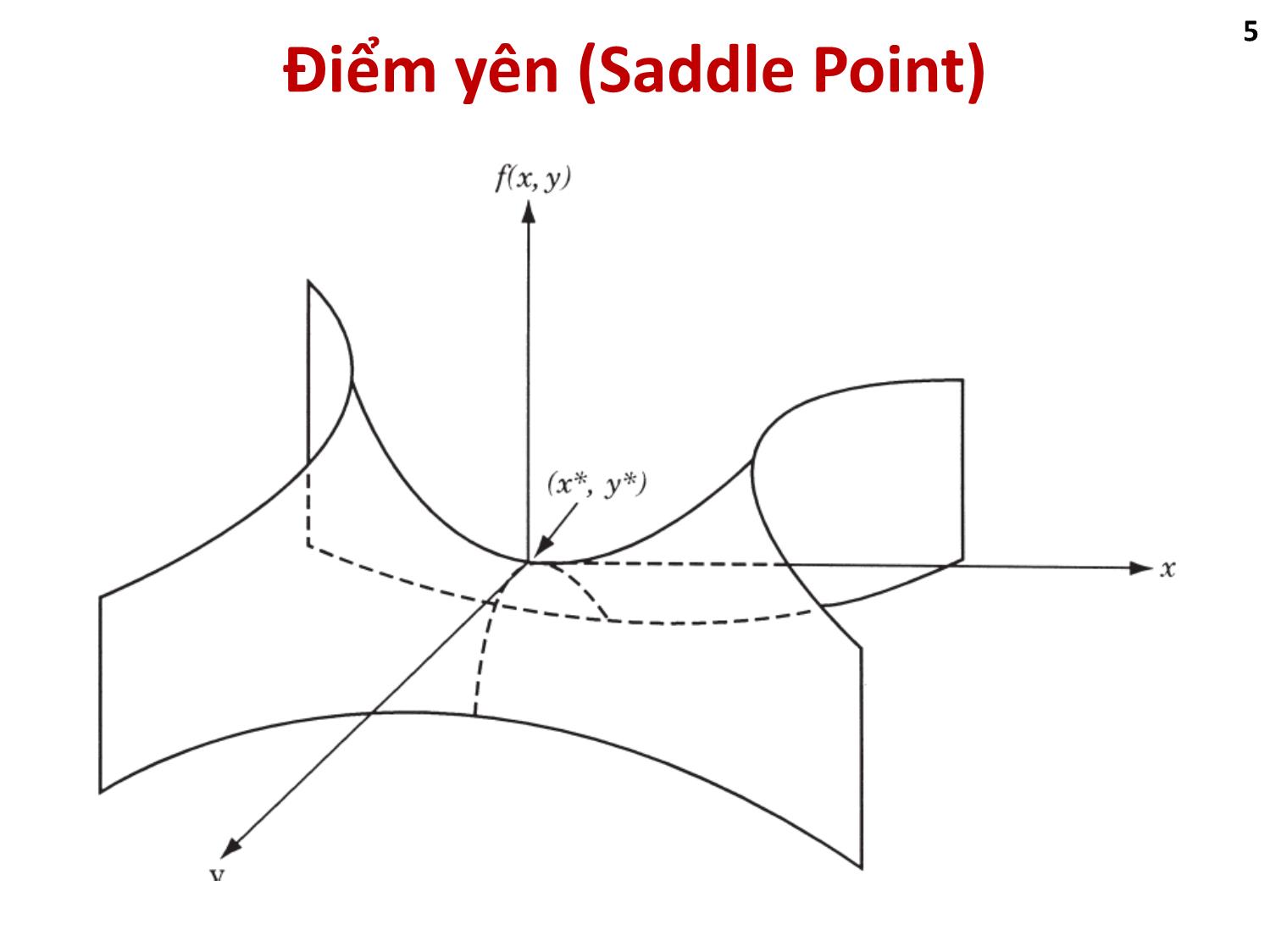
3. Nếu một vài Aj > 0 và 1 vài cái Aj < 0 hoặc = 0 x(i) – Điểm yên
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 3: Tối ưu hàm nhiều biến số không có ràng buộc trang 1
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 3: Tối ưu hàm nhiều biến số không có ràng buộc trang 2
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 3: Tối ưu hàm nhiều biến số không có ràng buộc trang 3
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 3: Tối ưu hàm nhiều biến số không có ràng buộc trang 4
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 3: Tối ưu hàm nhiều biến số không có ràng buộc trang 5
Tải về để xem đầy đủ hơn
File đính kèm:
bai_giang_toi_uu_hoa_trong_thiet_ke_co_khi_chuong_3_toi_uu_h.pdf
