Giáo trình Kinh tế lượng với các ứng dụng - Chương 9: Tương quan chuỗi
Phương pháp bình phương tối thiểu đã chứng tỏ mang lại các ước lượng về thông số có một vài
tính chất mong muốn, với điều kiện các số hạng sai số (ut) thỏa mãn một số giả thiết. Đặc biệt,
các ước lượng có tính không thiên lệch, nhất quán, và hiệu quả nhất. Khi một nhà nghiên cứu xử
lý dữ liệu dạng chuỗi thời gian, một số vấn đề đặc biệt phát sinh thường dẫn đến kết quả là vi
phạm vài giả thiết cần để phát ra những tính chất tốt đã liệt kê. Trong chương này, chúng ta sẽ
khảo sát một dạng vi phạm các giả thiết cơ bản về các số hạng nhiễu. Thứ nhất ta xem xét
những ẩn ý của việc bỏ qua sự vi phạm này và dùng thủ tục bình phương tối thiểu thường (OLS).
Ta có thể kỳ vọng rằng, như trong trường hợp phương sai của sai số thay đổi, vài tính chất có
thể không còn giữ được nữa. Thứ hai, ta kiểm định sự có mặt của sự vi phạm này, và cuối cùng
thảo luận các phương pháp có thể lựa chọn cho các vấn đề.
Giáo trình Kinh tế lượng với các ứng dụng - Chương 9: Tương quan chuỗi trang 1

Giáo trình Kinh tế lượng với các ứng dụng - Chương 9: Tương quan chuỗi trang 2
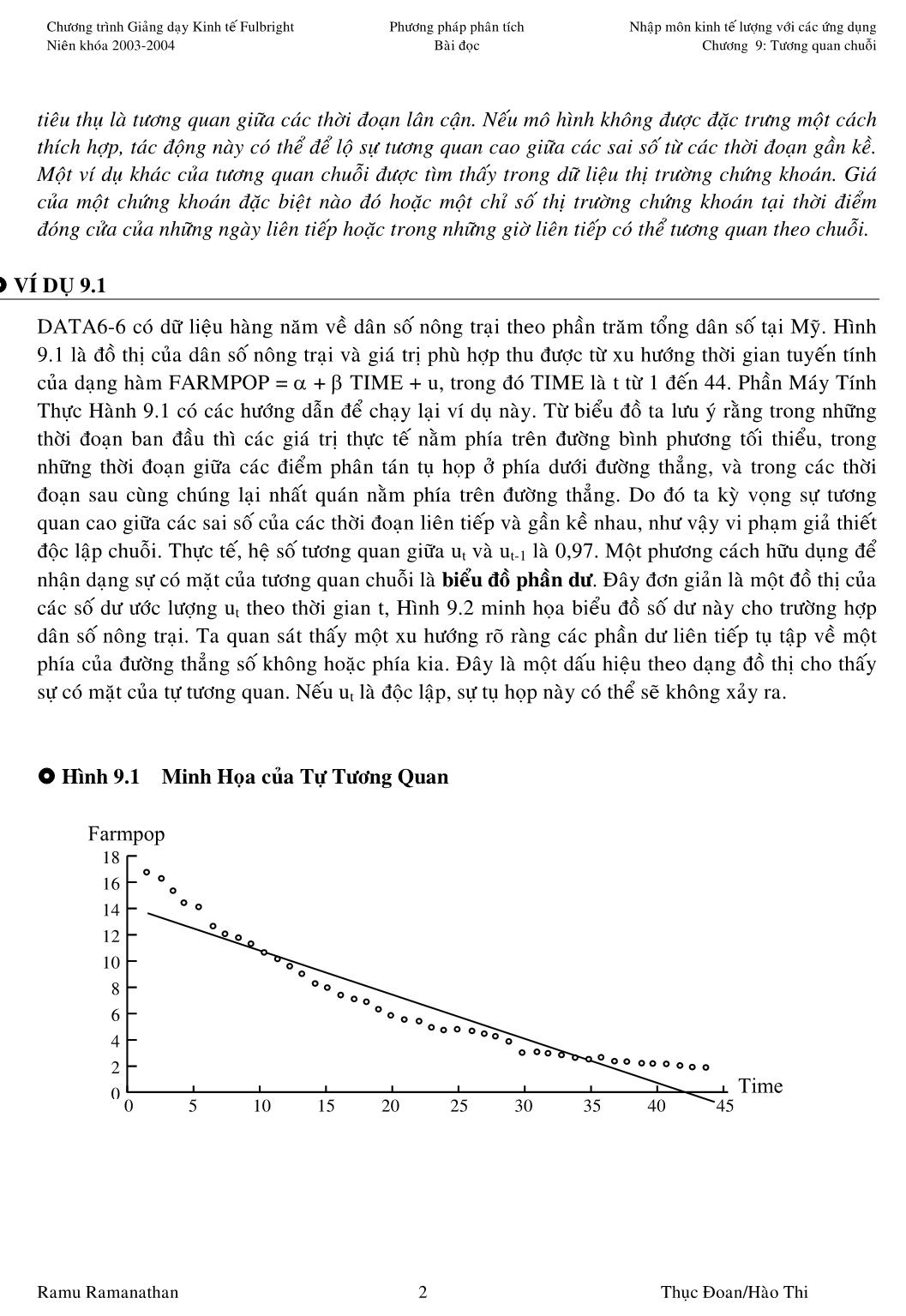
Giáo trình Kinh tế lượng với các ứng dụng - Chương 9: Tương quan chuỗi trang 3
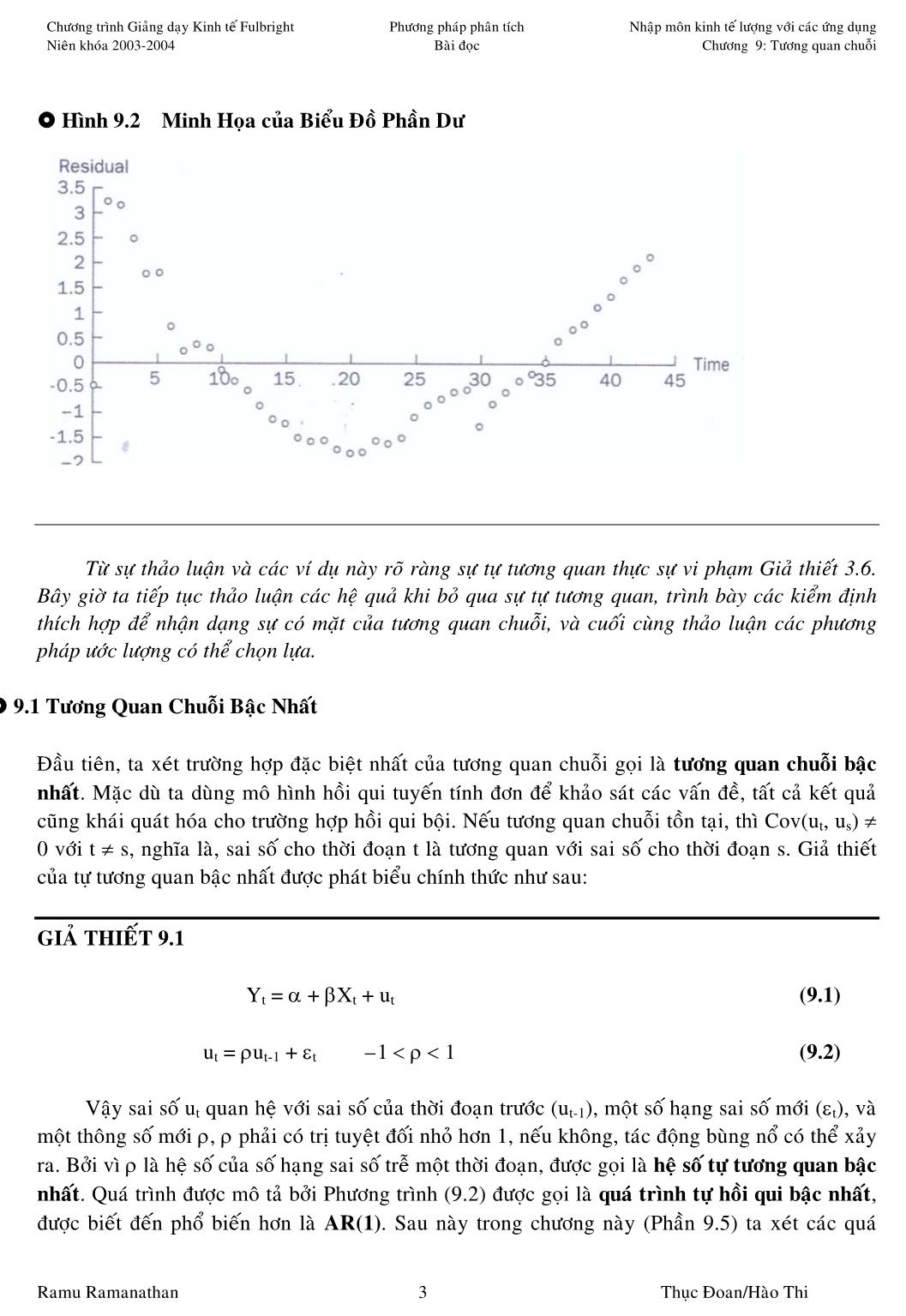
Giáo trình Kinh tế lượng với các ứng dụng - Chương 9: Tương quan chuỗi trang 4

Giáo trình Kinh tế lượng với các ứng dụng - Chương 9: Tương quan chuỗi trang 5
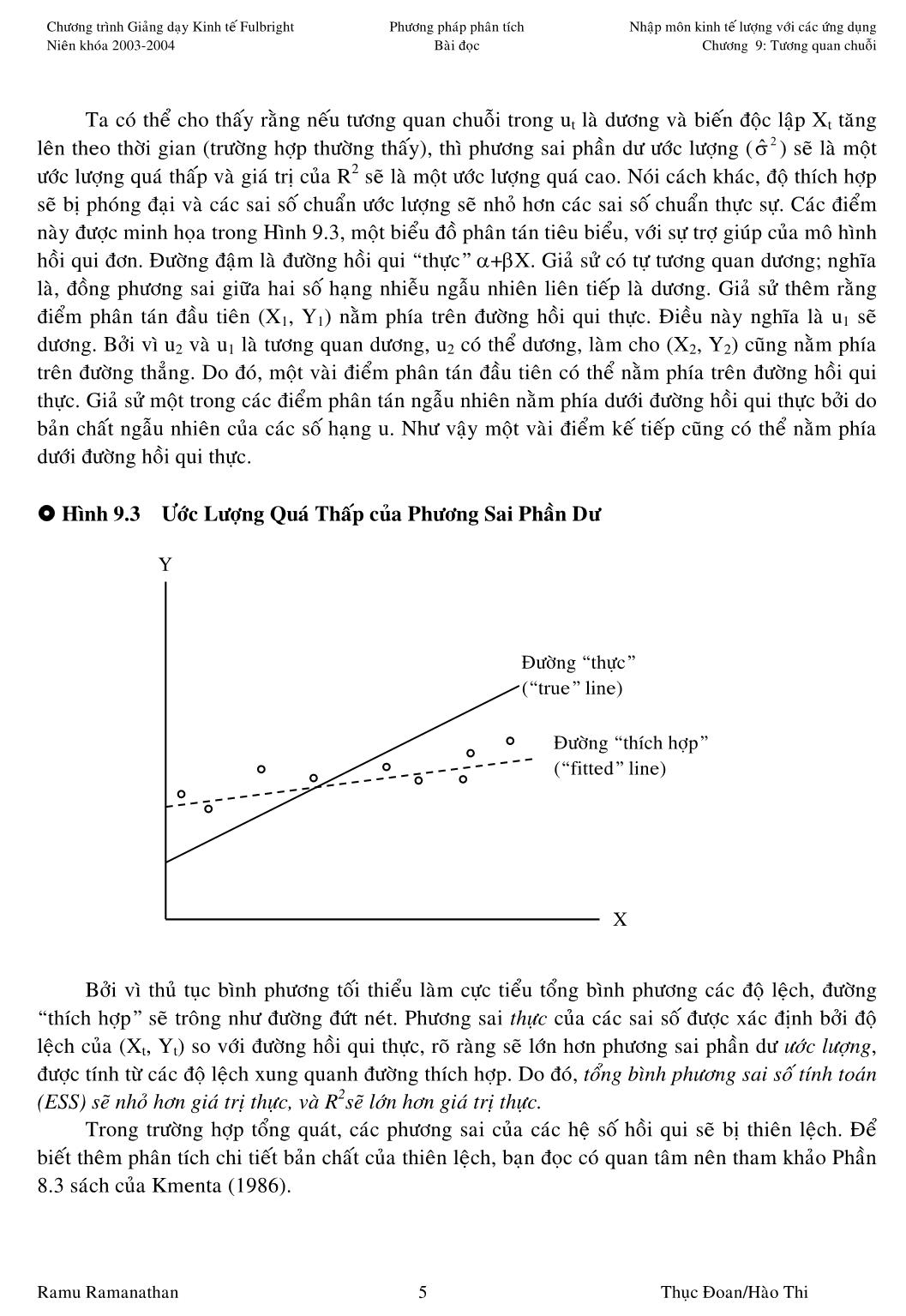
Tải về để xem đầy đủ hơn
File đính kèm:
 giao_trinh_kinh_te_luong_voi_cac_ung_dung_chuong_9_tuong_qua.pdf
giao_trinh_kinh_te_luong_voi_cac_ung_dung_chuong_9_tuong_qua.pdf



