Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 6: Tối ưu hàm nhiều biến số với ràng buộc tổng quát. Phương pháp cổ điển
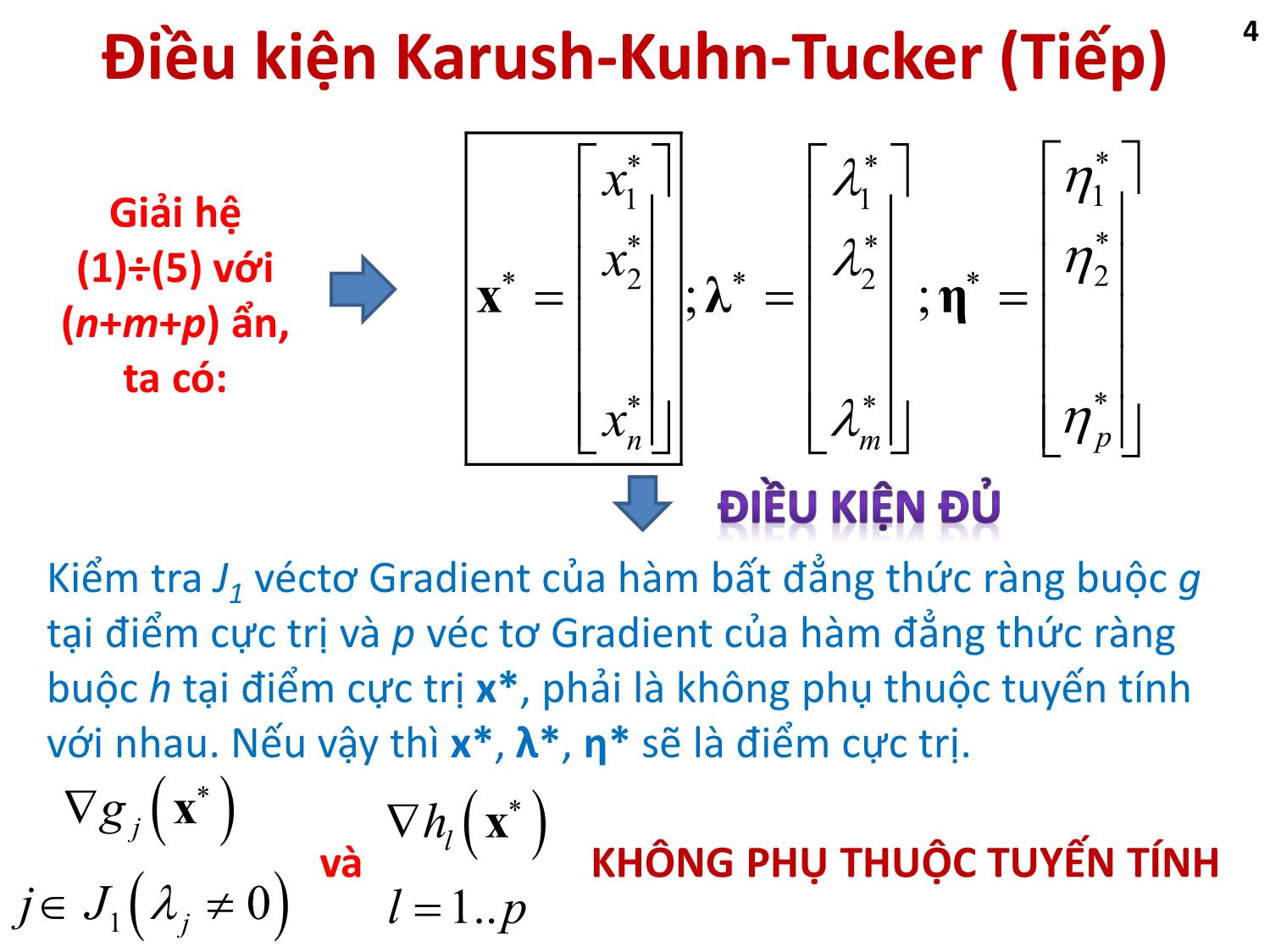
Kiểm tra J
1 véctơ Gradient của hàm bất đẳng thức ràng buộc g tại điểm cực trị và p véc tơ Gradient của hàm đẳng thức ràng buộc h tại điểm cực trị x*, phải là không phụ thuộc tuyến tính với nhau. Nếu vậy thì x*, λ*, η* sẽ là điểm cực trị.
Trường hợp 1: Khi M > N Các véc tơ sẽ luôn phụ thuộc tuyến tính
Trường hợp 2: Khi M = N Ta tính det(A). Nếu det(A) = 0 thì phụ thuộc tuyến tính, ngược lại thì không phụ thuộc tuyến tính.
Trường hợp 3: Khi M < N, Ta tính rank(A). Nếu rank(A)=M tức là bằng số lượng véc tơ thì hệ độc lập tuyến tính. Nếu khác rank(A)≠M thì hệ phụ thuộc tuyến tính.
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 6: Tối ưu hàm nhiều biến số với ràng buộc tổng quát. Phương pháp cổ điển trang 1
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 6: Tối ưu hàm nhiều biến số với ràng buộc tổng quát. Phương pháp cổ điển trang 2
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 6: Tối ưu hàm nhiều biến số với ràng buộc tổng quát. Phương pháp cổ điển trang 3
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 6: Tối ưu hàm nhiều biến số với ràng buộc tổng quát. Phương pháp cổ điển trang 4
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 6: Tối ưu hàm nhiều biến số với ràng buộc tổng quát. Phương pháp cổ điển trang 5
Tải về để xem đầy đủ hơn
File đính kèm:
bai_giang_toi_uu_hoa_trong_thiet_ke_co_khi_chuong_6_toi_uu_h.pdf
