Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 4: Tối ưu hàm nhiều biến số với ràng buộc đẳng thức. Phương pháp cổ điển
Có 3 phương pháp giải:
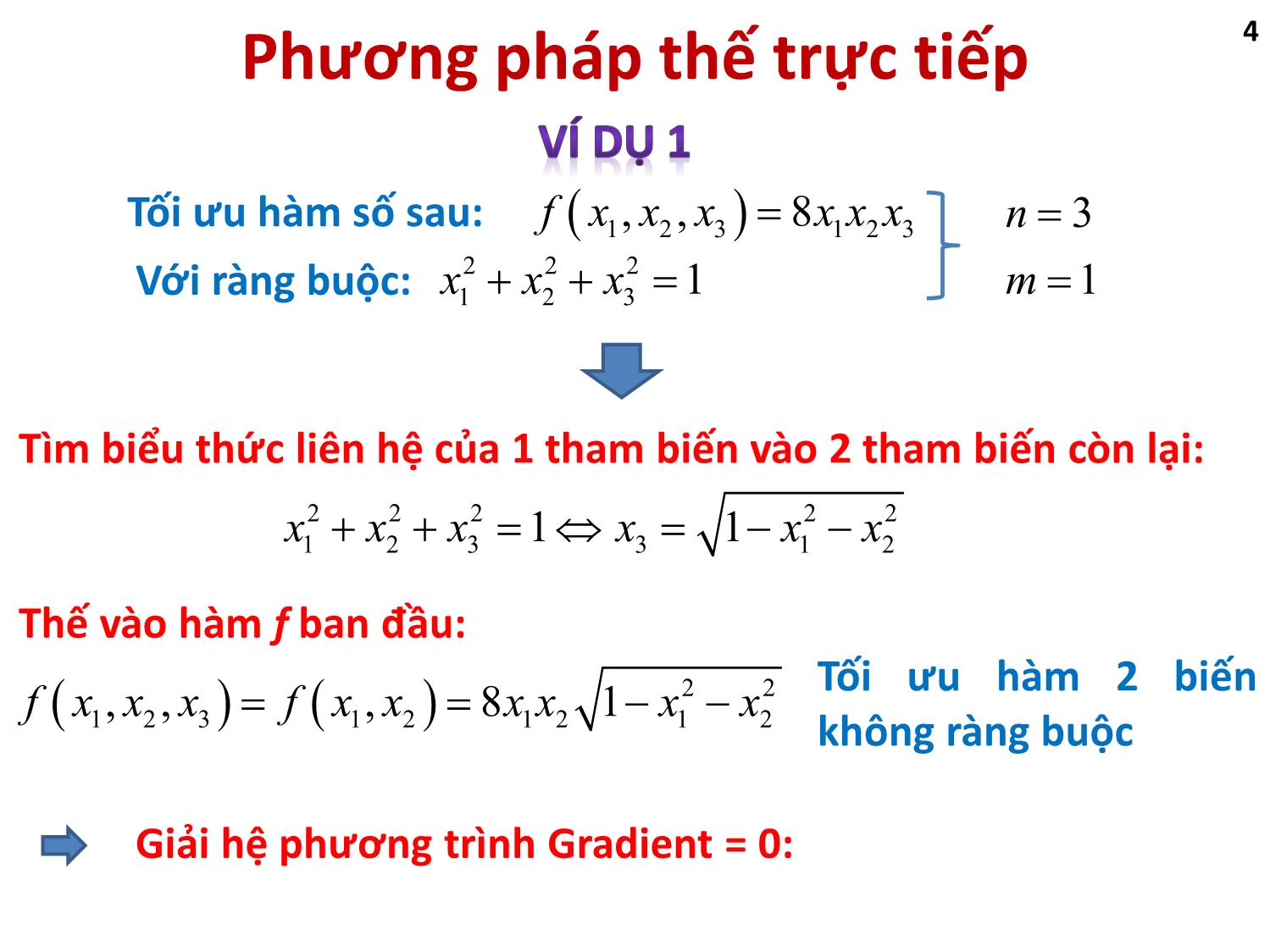
1. Phương pháp thế trực tiếp (direct substitution)
2. Phương pháp biến đổi ràng buộc (constrained variation)
3. Phương pháp nhân tử Lagrange (Lagrange multipliers)
Từ m ràng buộc đẳng thức, ta biến đổi và thu được các biểu thức tính m biến số thông qua (n-m) biến số còn lại (trong số n biến số tất cả). Từ đó thế vào biểu thức hàm f ban đầu. Như vậy hàm f sẽ trở thành hàm có (n-m) biến số nhưng không còn ràng buộc nào hết. Ta quay trở về bài toán tối ưu không ràng buộc.
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 4: Tối ưu hàm nhiều biến số với ràng buộc đẳng thức. Phương pháp cổ điển trang 1
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 4: Tối ưu hàm nhiều biến số với ràng buộc đẳng thức. Phương pháp cổ điển trang 2
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 4: Tối ưu hàm nhiều biến số với ràng buộc đẳng thức. Phương pháp cổ điển trang 3
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 4: Tối ưu hàm nhiều biến số với ràng buộc đẳng thức. Phương pháp cổ điển trang 4
Bài giảng Tối ưu hóa trong thiết kế cơ khí - Chương 4: Tối ưu hàm nhiều biến số với ràng buộc đẳng thức. Phương pháp cổ điển trang 5
Tải về để xem đầy đủ hơn
File đính kèm:
bai_giang_toi_uu_hoa_trong_thiet_ke_co_khi_chuong_4_toi_uu_h.pdf
