Bài giảng Thiết kế và đánh giá thuật toán - Bài 13: Đường đi ngắn nhất - Lê Nguyên Khôi
Trong đồ thị vô hướng G = (y,E)
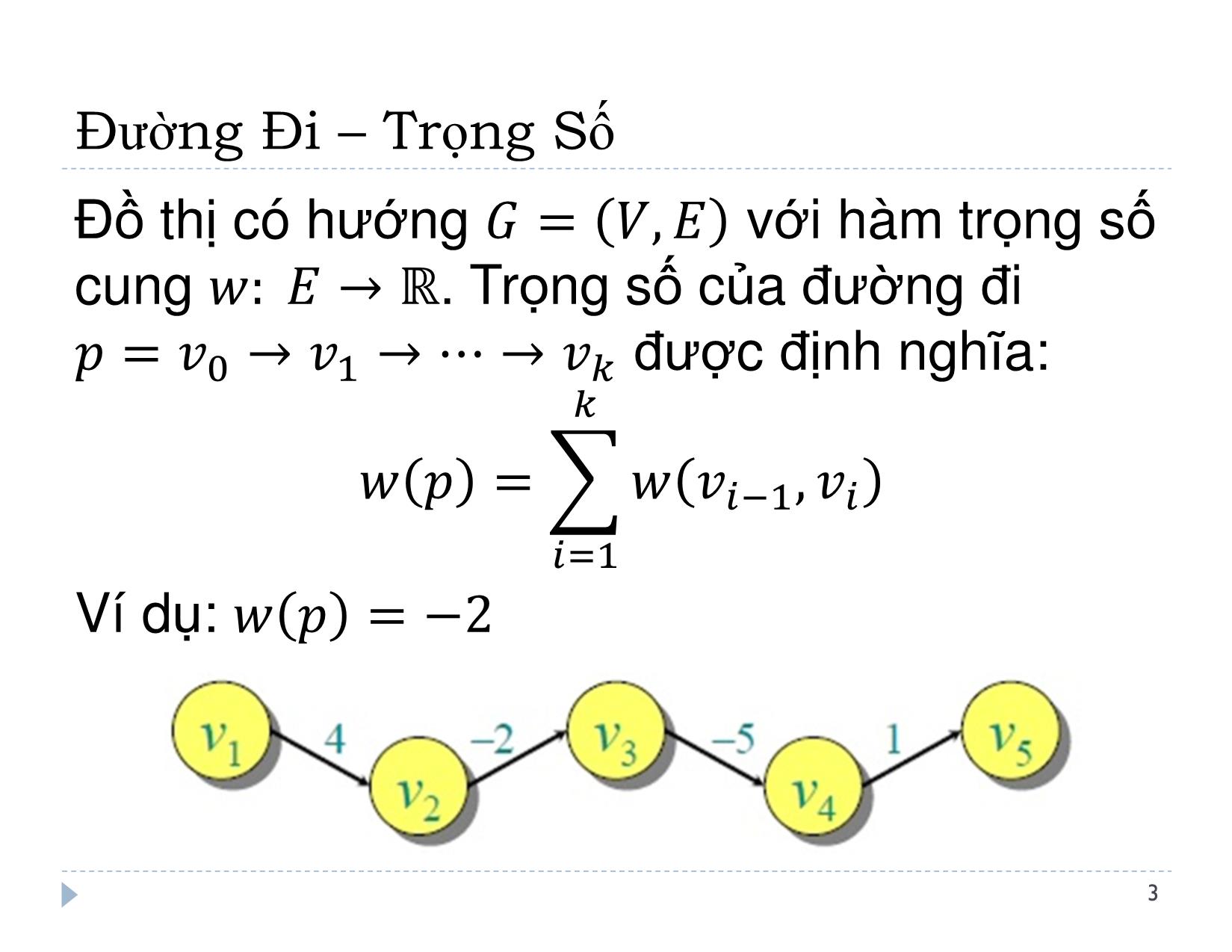
Đường đi
□ là dãy p các đỉnh v0> v2, - > vk
□ 2 đỉnh liên tiếp Vị, vi+1 được nối bởi 1 cạnh trong E. op được gọi là đường đi từ vr đến vk
Chu trình
□ là đường đi VQ, v2>. ,vk với k > 1
□ trong đó k đỉnh đầu tiên phân biệt và v0 = vk
Với đồ thị có hướng, trong một đường đi hay chu trình, 2 đỉnh liên tiếp (Vj, Vj+1) phai là mọt cung thuộc E
Bài giảng Thiết kế và đánh giá thuật toán - Bài 13: Đường đi ngắn nhất - Lê Nguyên Khôi trang 1
Bài giảng Thiết kế và đánh giá thuật toán - Bài 13: Đường đi ngắn nhất - Lê Nguyên Khôi trang 2
Bài giảng Thiết kế và đánh giá thuật toán - Bài 13: Đường đi ngắn nhất - Lê Nguyên Khôi trang 3
Bài giảng Thiết kế và đánh giá thuật toán - Bài 13: Đường đi ngắn nhất - Lê Nguyên Khôi trang 4
Bài giảng Thiết kế và đánh giá thuật toán - Bài 13: Đường đi ngắn nhất - Lê Nguyên Khôi trang 5
Tải về để xem đầy đủ hơn
File đính kèm:
giao_trinh_thiet_ke_va_danh_gia_thuat_toan_bai_13_duong_di_n.pdf
